物理学において, 電気と磁気に関する現象を扱う分野は電磁気学と呼ばれます.
電磁気学では, 単一の粒子の運動を記述する力学とは異なり,
無限自由度の空間の歪み(場)の運動が扱われます.
電磁場の運動を記述する方程式は,
19世紀末のMaxwellやHeavisideらの努力の結果,
現在では4つの美しい方程式にまとめあげられています.
驚くべきことに, 我々が目にする光も電磁場の振動であり,
これらの方程式に従って伝わります.

このように書くと, 方程式が1世紀以上前に定式化された電磁気学は
過去の学問のように感じられるかもしれません.
しかし, 電磁場の運動方程式は, その見掛けの単純さにも関わらず,
まだまだ多くの物理と応用が期待されています. これは,
電磁場と相互作用する物質の幾何学的配置の仕方に無限の自由度があるためです.

近年, こうした自由度を積極的に利用して設計されたメタマテリアルと呼ばれる人工媒質が注目されています.
メタマテリアルは, 人工的に金属や誘電体を組み合わせて作ったメタアトムから構成されます.
各メタアトムは人工的な原子として働きます. メタアトムの設計を工夫することにより,
通常の原子では実現できなような電磁応答を示すメタマテリアルを創り出すことができます.
このような考えのもとで, 負の屈折率を持った媒質や, 透明マント,
回折限界を越えた解像度を持つ完全レンズなど,
通常は考えられないような波動伝搬を示すメタマテリアルが実現されてきました[1].

こうしたメタマテリアルの発展に伴い,
電磁気学の基礎にも再び焦点が当たりつつあります.
近年, 電磁気学の構造が, Bossavitらにより幾何学的視点から見直されつつあり,
数値計算分野では大きな成功を収めています[2].
さらに, 電磁気学の幾何学化を押し進め,
電磁気学を一般相対性理論における計量と切り離し,
逆に電磁気から重力情報を取り出そうとするpremetric
electrodynamicsなる立場も提案されています[3].

このような電磁気学の状況下で, 私は特に, 新たなメタマテリアル設計手法,
および, 電磁気学の幾何学化に大きな関心を持ち,
理論・計算機シミュレーション・実験のすべての観点から研究を行なっています.
以下にこれまでの結果の一部を示します.

量子力学アナロジを利用したメタマテリアル設計[4]

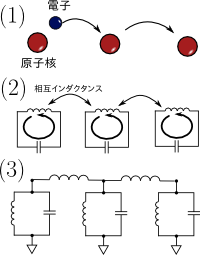
従来のメタマテリアル研究においては，メタアトム間に結合がない場合が主に扱われてきました．
しかし，それらの間に結合があると, 多重モードやバンド形成など様々な現象が生じます．
これは量子力学で記述される固体中の電子の振る舞いと似ています.
メタアトムとして，金属構造が用いられる場合,
メタマテリアルは回路モデルで記述されます.
このため, 回路と電子とのアナロジを定式化しておくことが,
メタマテリアル設計を行う上で重要となります.
そこで, 本研究では, 電子のタイトバインディングモデルのアナロジを回路に対して定式化しました.
たとえば, 右図に示す異なる3つのシステムは同じ共振応答を示します.
以上の結果を用いて, 電子系と同じ応答を示す回路モデルを構築し, その回路モデルに従ってメタマテリアルを設計することで,
電子系と同じバンド構造を持ったメタマテリアルを作り出すことが可能になります.

金属カゴメ格子におけるフラットバンドの観測[5]

カゴメ格子上の電子は, 平坦な分散関係(フラットバンド)を持つことが知られています.
これは物理的には, 電子波の干渉の結果, 閉じ込めが起こり, 各モードがデカップルする結果,
生じます. フラットバンドは, 遍歴電子強磁性や, ボソンの超固体相の形成など,
多彩な現象を引き起こすと考えられており, 固体物理学では大きく注目されています.
東京大学の遠藤氏は, 電磁系でもカゴメ格子型の金属導波路網に対して,
フラットバンドができることを理論的に示しています(彼が学部生の頃に!)[5].

しかし, 電磁系でのフラットバンドはこれまで実験的に観測されておらず,
その実現が課題でした.
遠藤氏の系は, 2次元の理想化された系で実験によって直接確かめるのは困難でした.
この問題を解決するため, 私は, 回路と量子のアナロジを利用して, より簡単な平面構造でも,
フラットバンドが生じることを理論的に示しました. さらに, テラヘルツ領域で,
フラットバンドが形成されていることを実験的に示すことにも成功しました(下図).
フラットバンドの閉じ込め効果を応用すると, 光メモリや, 非線形性の増強,
高感度センシング・イメージングが可能になると期待できます.

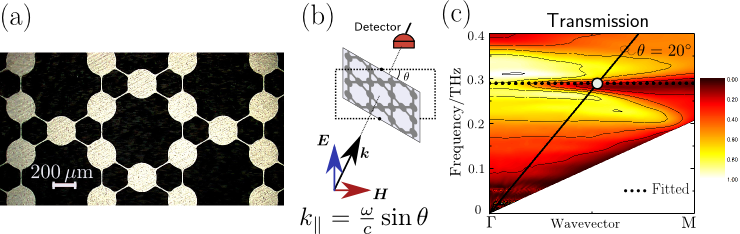
説明: (a) 作成した金属カゴメ格子 (b) 透過実験の配置 (c) 得られたフラットバンド